피보나치 수 구현하기
피보나치 수를 구현하는 방법에는 두 가지가 있습니다.
- 재귀함수를 사용하는 방법
- 반복문을 사용하는 방법
피보나치 수란?
피보나치 수는 다음과 같이 정의되는 수열입니다.
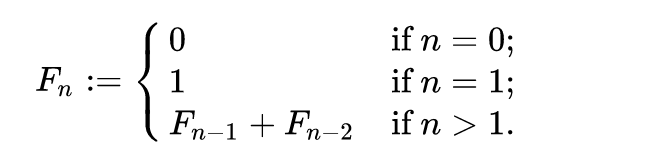
fibonacci 수열은 0 1 1 2 3 5 8 13... 입니다. 앞에 있는 두 수를 더하여 그 다음의 수를 얻을 수 있습니다.
첫 번째 수와 두 번째 수는 0 과 1 로 정해져있습니다.
그 다음 n 번 째 피보나치 수는 (n-1 번 째 피보나치 수)+(n-2 번 째 피보나치 수)입니다.
재귀함수로 피보나치 수 구현하기
피보나치 수를 재귀함수로 구현하면 다음과 같습니다.
function fibonacci(num) {
if (num === 1) {
return 0;
}
if (num === 2) {
return 1;
}
return fibonacci(num - 1) + fibonacci(num - 2);
}
5 번째 피보나치 수를 계산하는 과정을 그림으로 표현하면 다음과 같습니다.
fib(5)
/
fib(4) fib(3)
/ /
fib(3) fib(2) fib(2) fib(1)
/
fib(2) fib(1)
fibonacci(5)는 fibonacci(4) + fibonacci(3)을 계산하기 위해 fibonacci(4)를 호출합니다. 이처럼 자기 자신을 호출하는 함수를 재귀함수라고 합니다.
fibonacci(4)는 fibonacci(3) + fibonacci(2)를 호출합니다.
fibonacci(3)은 fibonacci(2) + fibonacci(1)를 호출합니다. 여기서 fibonacci(2) 와 fibonacci(1)의 값은 1 과 0 으로 정하였으므로 더이상 함수를 부르지 않고 값이 계산되어 나오게 됩니다. fibonacci(3)은 0+1 인 1 이 됩니다.
그 다음 fibonacci(4)를 계산하려고 호출했던 fobonacci(2)를 계산합니다. fibonacci(4)는 계산이 완료 되고 다시 fibonacci(3)을 계산합니다. 위와 같은 과정을 거쳐야 fibonacci(5)를 구할 수 있습니다.
만약 fibonacci(5)가 아닌 fibonacci(100), fibonacci(1000)이면 어떨까요?
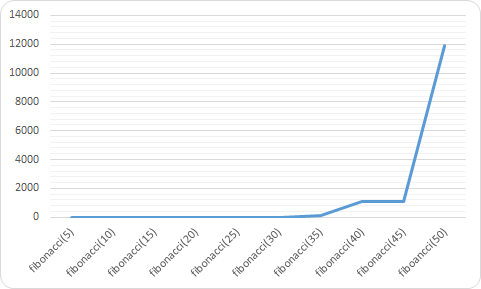
5 번째 피보나치 수를 구하기 위해서는 함수를 9 번 호출해야 합니다. 10 번째 피보나치 수는 109 번, 20 번 째 피보나치 수는 13529 번, 30 번 째 피보나치 수는 1664079 번 함수를 호출해야 합니다.
다음은 피보나치 수를 구하는 함수의 실행시간 그래프입니다. 구하려는 피보나치 수가 커질수록 급격하게 그래프가 치솟는 것을 볼 수 있습니다.
함수 스택
피보나치 수가 커질수록 함수 실행시간이 급격히 증가하는 이유는 무엇일까요 함수가 계산되는 방식때문입니다.
함수가 호출 될 때 메모리블록을 할당받게 됩니다. 이 블록들이 쌓이는 곳을 스택프레임이라고 합니다. 함수가 return 되면 할당받았던 메모리블록은 스텍프레임에서 사라지게 됩니다. 함수는 가장 나중에 넣은 메모리블록이 가장 먼저 나오는 LIFO(last in first out)의 구조입니다.
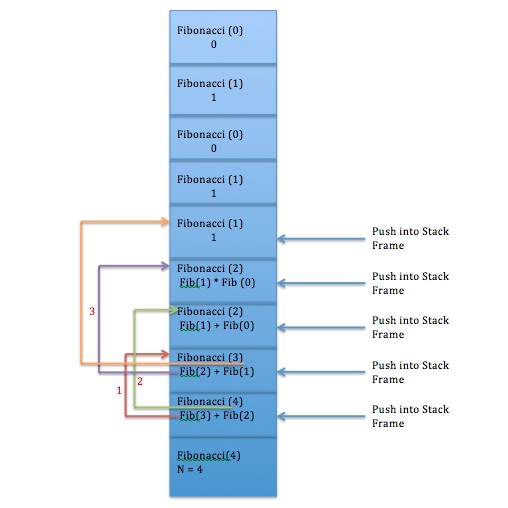
n 번 째 피보나치 수를 계산 할 때 스텍프레임에 메모리블록들이 쌓이다가 fibonacci(2)와 fibonaci(1)이 나와야만 미리 약속한 값인 0 과 1 로 꺼낼 수 있습니다. 그러나 한 번 꺼낸 값이 스택에 저장되는 것이 아닙니다. 계산이 끝나 return 하게 되면 기존에 선언한 변수는 스택에서 사라지게 됩니다. 그렇기 때문에 그 전에 fibonacci(3)을 계산하였어도 다시 한번 함수를 불러 계산해야 합니다.
반복문으로 피보나치수 구하기
피보나치 수를 구하는 또다른 방법은 반복문을 사용하는 것 입니다. 반복문을 이용하여 n 번째 피보나치 수를 구하면 대략 n 번만 반복하여 결과를 얻을 수 있습니다. 재귀함수를 사용하는 것 보다 훨씬 더 효율적입니다. 이제 100 번 째 1000 번째 피보나치수를 구하더라도 브라우저가 멈추지 않을 것 입니다.
반복문을 사용한 피보나치 함수를 구현하면 다음과 같습니다.
function fibonacci(num) {
if (num === 1) {
return 0;
}
if (num === 2) {
return 1;
}
var prepre = 0;
var pre = 1;
var fib;
for (i = 2; i < num; i++) {
fib = pre + prepre;
prepre = pre;
pre = fib;
}
return fib;
}
지금까지 재귀함수와 반복문, 두 가지 방법으로 피보나치 수를 구현해 보았습니다.
재귀함수를 사용하는 방법이 직관적이고 이해하기 쉬운 방식이지만 수가 커질수록 스택의 깊이는 깊어지고 함수 실행 시 많은 시간이 소요됩니다. 이런 문제점 때문에 재귀함수를 사용하는 대신, 반복문을 사용하여 필요한 값을 계속해서 변수에 저장하는 방식으로 피보나치 수를 구현하였습니다.
단순히 함수를 구현하여 결과를 얻는 것뿐만 아니라 그 과정의 비용도 생각해야 합니다.
